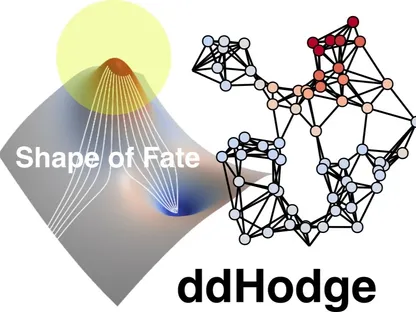
طوّر باحثون من جامعة كيوشو اليابانية، طريقة حسابية مبتكرة تحمل اسم ddHodge، قادرة على إعادة بناء الديناميكيات المعقدة، التي تحكم كيفية اتخاذ الخلايا لقرارات مصيرها، مثل التحول إلى خلايا عصبية أو عضلية.
ووفقاً لدراسة نشرت في دورية Nature Communications، تمثل هذه الطريقة تقدماً نوعياً في فهم العمليات البيولوجية المرتبطة بالتطور الجنيني، وتجديد الأنسجة، وتطور الأمراض.
ويعد فهم كيفية اختيار الخلايا لمساراتها التطورية أحد أكثر التحديات تعقيدا في علم الأحياء والطب. فخلال التطور الجنيني، أو عند إصلاح الأنسجة التالفة، تمر الخلايا بسلسلة من التحولات الدقيقة في حالتها الوظيفية، تقودها في النهاية إلى مصير محدد. ولمتابعة هذه التحولات، يعتمد العلماء على تقنية تسلسل الحمض النووي الريبي أحادي الخلية التي تكشف عن الجينات النشطة داخل كل خلية على حدة.
غير أن هذه التقنية، رغم قوتها، تعاني من قيد أساسي يتمثل في كونها تقنية مدمرة، إذ لا تتيح سوى "لقطة ثابتة" لحالة الخلية في لحظة زمنية واحدة، دون إمكانية تتبع تطورها عبر الزمن.
"حالة الخلية".. مشكلة جوهرية
على مدار السنوات الماضية، ظهرت أساليب حسابية تحاول تجاوز هذا القيد، من بينها تقنية "سرعة الحمض النووي الريبي" التي تستنتج الاتجاه المستقبلي القريب لحركة الخلية وسرعة تقدمها نحوه.
لكن هذه المقاربات تصطدم بمشكلة جوهرية، فـ"حالة الخلية" لا تُعرّف بواسطة عدد محدود من المتغيرات، بل من خلال نشاط آلاف الجينات، ما يضعها في فضاء عالي الأبعاد شديد التعقيد.
ولجعل البيانات قابلة للتحليل، تضطر الطرق التقليدية إلى ضغط هذا الفضاء في عدد أقل من الأبعاد، الأمر الذي يؤدي حتماً إلى فقدان معلومات هندسية مهمة. ونتيجة لذلك، يصبح من الصعب- بل من المستحيل- التمييز بدقة بين خلية غير مستقرة وقابلة للتغير عند نقطة تفرع، وأخرى مستقرة وملتزمة بمصير محدد.
وقدّم الباحث المشارك "كازوميتسو ماهارا" من كلية العلوم الطبية بجامعة كيوشو، بالتعاون مع "ياسويوكي أوكاوا" من معهد التنظيم الحيوي الطبي بالجامعة نفسها، إطار ddHodge بوصفه حلاً يحافظ على الهندسة الأصلية للبيانات عالية الأبعاد، ويتيح إعادة بناء ديناميكيات حالة الخلية بدقة أعلى بكثير من الطرق المتاحة سابقاً.
مكونات رئيسية
يستند ddHodge إلى مفهوم رياضي متقدم يعرف بتحليل هودج، وهو مبرهنة قوية في الرياضيات الحديثة تسمح بتفكيك الحركة أو التدفقات في أي نظام معقد إلى مكونات أساسية قابلة للقياس.
وفي تطبيقه على بيانات الخلايا، يقسم الإطار حركة الخلايا عبر "منظر" الحالات الممكنة إلى ثلاثة مكونات رئيسية.
المكون الأول هو التدرج، ويمثل التدفق الاتجاهي العام الذي تقوده الخلايا نحو حالات مستقرة، أما المكون المتبقي فيتضمن الالتفاف والمكون التوافقي وهما يعكسان الحركات الدورية أو الدورانية، مثل تلك المرتبطة بدورة الخلية.
ويشرح "ماهارا" أن خلفيته في العلوم الإحصائية لعبت دوراً محورياً في تطوير هذه الفكرة، إذ تعرف خلال دراسته العليا على أسلوب "هودج" المستخدم في مسائل الترتيب والتصنيف، مثل خوارزميات ترتيب الصفحات على الإنترنت.
وعندما انتقل لاحقاً إلى أبحاث علوم الحياة، أدرك أن الفكرة الرياضية ذاتها يمكن أن تسهم في تفسير الانتقالات المعقدة بين حالات الخلايا في بيانات التسلسل أحادي الخلية.
ويعتمد إطار ddHodge على تمثيل قائم على الرسوم البيانية لحالات الخلايا في فضاء عالي الأبعاد، مع الحفاظ على الهندسة المحلية للبيانات.
وبهذا الأسلوب، يمكن قياس خصائص ديناميكية أساسية مثل الاستقرار، والتباعد، والمكونات الدورانية، دون التضحية بالمعلومات البنيوية التي غالباً ما تضيع عند تقليل الأبعاد.
ويظهر التصور المفاهيمي للطريقة منظراً شبيهاً بسطح طاقة، حيث تمثل الخطوط البيضاء مسارات حركة الخلايا عبر الزمن. وعلى الرغم من أن بيانات تقنية تسلسل الحمض النووي الريبي أحادي الخلية تلتقط فقط لقطات زمنية منفصلة، فإن ddHodge ينجح في "إعادة بناء" هذه اللحظات المحلية معاً لتكوين صورة عالمية متماسكة للديناميكيات الخلوية.
بيانات متنوعة
وعند تطبيق ddHodge على بيانات تقنية تسلسل الحمض النووي الريبي أحادي الخلية لنحو 46 ألف خلية جنينية من الفأر، كشف الباحثون أن أكثر من 88% من ديناميكيات التعبير الجيني خلال المراحل المبكرة من التطور الجنيني يمكن تفسيرها بواسطة مكون التدرج وحده. ويؤكد هذا التحليل، استناداً إلى بيانات واقعية، المفهوم الكلاسيكي في علم الأحياء التطوري الذي يفترض أن الخلايا تتمايز عبر التحرك نحو حالات مستقرة، مع الابتعاد عن نقاط التفرع غير المستقرة.
وأتاح التركيز على هذه النقاط غير المستقرة للباحثين تحديد جينات محورية تلعب دوراً في دفع الخلايا نحو الاستقرار أو الحفاظ عليه أثناء التزامها بمسار تطوري معين.
ولم يقتصر تقييم ddHodge على البيانات التجريبية فقط، بل شمل أيضاً محاكاة بيانات متنوعة. وأظهرت هذه الاختبارات أن الإطار قادر على إعادة بناء ديناميكيات حالة الخلية بشكل موثوق حتى في وجود بيانات جزئية أو مشوشة، مع دقة تفوق الأساليب التقليدية بنحو مئة مرة. وتبرز هذه النتيجة قوة الطريقة في التعامل مع التحديات الواقعية التي تواجه تحليل البيانات البيولوجية واسعة النطاق.
ويشير الباحثون إلى أن ddHodge يوفر وسيلة كمية لتحديد "اللحظات الحرجة" في حياة الخلية، مثل التوقيت والمكان الدقيقين لاتخاذ قرار المصير. فالإطار لا يحدد الاتجاه الذي تتحرك فيه الخلايا فحسب، بل يصف أيضاً سرعة هذا التغير ومدى استقراره داخل فضاء عالي الأبعاد. ومن المتوقع أن يسهم ذلك في تعميق فهم طيف واسع من الظواهر البيولوجية، بما في ذلك التطور الجنيني، وتجديد الأنسجة، وتقدم السرطان.
توظيف الرياضيات الحديثة
وتتجاوز تطبيقات ddHodge المجال الطبي الحيوي، بحسب القائمين على الدراسة. إذ يرون أن الإطار الحسابي ذاته يمكن توظيفه لفهم عمليات معقدة أخرى تتغير بمرور الزمن، مثل تدهور المواد، وأنماط المناخ، وحتى السلوكيات الاجتماعية والاقتصادية.
وفي جميع هذه الحالات، تكمن المشكلة في التعامل مع بيانات ضخمة عالية الأبعاد، حيث يصعب استخلاص البنية الديناميكية الكامنة دون فقدان معلومات أساسية.
ويجسد ddHodge، في هذا السياق، مثالاً واضحاً على كيفية توظيف مفاهيم من الرياضيات الحديثة- كالهندسة التفاضلية والحوسبة العددية- لخدمة تحديات عملية في علوم الحياة وغيرها من المجالات. ومن خلال الحفاظ على الهندسة الأصلية للبيانات، يفتح هذا الإطار الباب أمام رؤى جديدة كانت ستظل خفية لولا هذا الدمج بين الرياضيات المتقدمة والتحليل البيولوجي.
وبينما لا يزال الإطار في مراحله الأولى من حيث الانتشار والتطبيق، فإن الباحثين يتوقعون أن يصبح أداة داعمة في تحليل مجموعات البيانات الضخمة المستخدمة في مسارات اكتشاف الأدوية والصناعات الحيوية، فضلاً عن إمكاناته في الكشف المبكر عن حالات خلوية مرتبطة بالأمراض أو بعمليات التجديد.
وبهذا، لا يقدم ddHodge مجرد تقنية تحليلية جديدة، بل يمثل خطوة نحو فهم أعمق لديناميكيات الحياة على مستوى الخلية، من خلال عدسة رياضية دقيقة تحافظ على تعقيد الواقع بدل تبسيطه.